A májusi érettségi vizsgára való tekintettel öt részes matematikai felkészítő sorozattal segítünk minden érettségi előtt álló diáknak! Az első részben általánosságban bemutattuk milyen feladatok fordulnak elő a vizsgán, míg a második részben a kamatos kamat kiszámítását mutattuk be neked. Harmadik bejegyzésünk a középérték világába kalauzol el téged!
A ballagás utáni érettségi időszak a diákok életében fontos eseménynek számít! Egyesek joggal félnek tőle, hiszen megfelelő tudás hiányában írják meg a vizsgát. Az alapvető témakörök ismerete nélkül rengeteg pontot veszíthetnek a végzős hallgatót. Például sok diákot érdekli, azonban nem tudják, hogy a félévi vagy az év végi eredményeik átlaga milyen módon számítható ki. Aki eddig nem boldogult vele, a Tantaki segítségével most megtanulhatja, hogyan számolhatunk középértékeket!
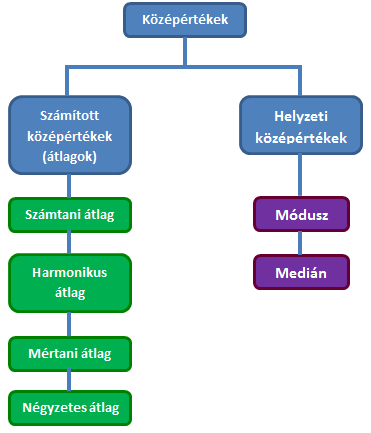
Középérték
Ha meg akarunk vizsgálni valamit, akkor a vele kapcsolatos számadatok, illetve a tulajdonságaik sok hasznos tájékoztatást adhatnak. Ezen adatok rendezése, csoportosítása nagymértékben megkönnyíti az információk feldolgozását és átláthatóságát.
A számadatok lehetővé teszik, hogy általuk megfelelő jellemzést készítsünk. A számadatokból számított, átlaggal becsülhető érték a középérték. Tehát a középérték az azonos fajta adatok tömegének számszerű jellemzője.
Többféle számítási módszer van erre, például: átlag, mértani közép, harmonikus közép, négyzetes közép stb.
Mutasd meg a Facebookon Te is az ismerőseidnek a cikket, kattints a gombra:
Aritmetikai közép/átlag:
![]()
Geometriai/mértani közép:
![]()
Közeleg az érettségi vizsga időpontja! Gyermeked minden témakörben otthonosan érzi magát? Nem érti, hogyan kell megoldani a másodfokú egyenletet? Kattints a képre, és próbáljátok ki az Érettségi felkészítő DVD-lemez demó verzióját!

Kattints ide és próbáld ki most ingyenes a felkészítő lemez demó változatát!
Példafeladat
Mennyi az 50 és a 72 számtani és a mértani közepe?
Megoldás
A számtani közép (más néven átlag) a két szám összege osztva kettővel:
![]()
Először a számláló (a tört felső tagja) 2 számát adjuk össze, majd az így kapott értéket elosztjuk a nevezővel (tört alsó tagja). A dolog lényege, hogy a számlálóba kerülnek azok a számok, amiknek az átlagára vagyunk kíváncsiak, míg a nevezőbe az a szám kerül, ami megadja, hogy hány adatnak az átlagára vagyunk kíváncsiak.
A mértani közép a két szám szorzatának a négyzetgyöke:
![]()
Először a gyök alatti 2 számot kell összeszoroznunk, majd az így kapott számból gyököt vonunk, és megkapjuk az eredményt. Mértani közepet akkor használunk, amikor az átlagolandó értékek között sorozatszerű kapcsolat van.
Gyermeked tanulási nehézségekkel küszködik? Kattints a képre és ingyenes e-mailes tippeket kaphatsz!
Tehát mostantól gyermekednek sem okozhat gondot az év végi jegyek átlagának kiszámítása!
Következő bejegyzésünk február harmadikán jelenik meg és a szinusz-tétel helyes alkalmazását mutatja majd be.
Tetszett a cikk? Mutasd meg ismerőseidnek, kattints a megosztás gombra:
Nagy Erika
a játékos tanulás szakértője
