Érettségire felkészítő sorozatunk keretében egy-egy témakört alaposabban bemutatunk nektek! A kamatos kamat és a középérték után most a szinusztétellel foglalkozunk.
A matematika egyik kiemelt része a geometria. A májusi érettségin évről évre mindig előfordul pár példafeladat a témával kapcsolatban: háromszög szögeinek, gúla térfogatának kiszámítása és még sorolhatnánk. Amennyiben gyermeked kevésbé szereti a geometriát, a Tantaki segítségével megszeretheti!
Az első és legfontosabb sokszög, amivel megismerkedhetünk a háromszög. Több fajtája van, ettől függően eltérő nagyságú szögeket tartalmazhatnak. Léteznek módszerek, amivel kiszámíthatóak a háromszög hiányzó szögei és oldalai.
Érettségire felkészítő lemezünkön a geometria mellett az összes témakör példákkal, megoldás levezetésekkel található meg. Kattints a képre és próbáld ki most ingyenesen a matek tananyag demó változatát!

Kattints a linkre és próbáld ki most a tananyag demó változatát!
Szinusztétel
A szinusztétel egy geometriai tétel, amely kimondja, hogy egy bármilyen háromszög oldalainak aránya egyenlő a szemközti szögek szinuszainak arányával. Például egy háromszögnek 2 belső szögét, de csak 1 oldalát ismerjük. A hiányzó adatokat könnyedén kiszámíthatjuk a szinusztétel segítségével. Felírva:
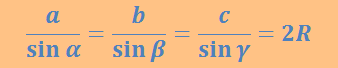
Mutasd meg a Facebookon Te is az ismerőseidnek a cikket, kattints a gombra:
Példafeladat
Egy háromszög egyik oldala 11 cm, a rajta fekvő két szög 73° és 87°. Mekkora a másik két oldal?
Megoldás
Szinusztétellel számolhatunk, de ehhez ismerni kell a harmadik szöget.
Ezt megkapjuk, ha a két ismert szöget kivonjuk a 180°-ból:
180° − 73° − 87° = 20°, mivel a háromszög belső szögeinek összege összesen 180°!
Két oldal aránya megegyezik a velük szemközti szögek szinuszának arányával. Felírva:
![]()
Helyettesítsünk be, és számoljuk ki a b oldalt!
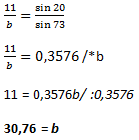
Ugyanígy tudjuk kiszámolni a c oldalt:
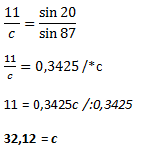
A háromszög másik két oldala 30,76 cm és 32,12 cm hosszú.
A szinusztételt mostantól bármikor tudja alkalmazni a gyermeked, így érettségin sem okozhat már neki problémát! Az egyik legkönnyebben alkalmazható tétel a geometriában, amit ráadásul gyermeked is könnyen elsajátított a Tantaki segítségével!
Szeretnél ingyenes e-mailes tippeket kapni? Nincs más dolgod, mint rákattintani a képre!
Nagy Erika
a játékos tanulás szakértője
Tetszett a cikk? Mutasd meg ismerőseidnek, kattints a megosztás gombra:
