Kedves Szülőtársak!
Sokat beszélgetek, koordinálok más szülőkkel és szakértőkkel is a témában, hogy minél többféle helyzettel találkozzak és minél többféle problémára találjak megoldást, hiszen a gyerek problémája a mi problémánk is.
Sok-sok szituáció megfigyelése után észrevettem egy közös nevezőt az úgy nevezett „nehéz tárgyakkal” kapcsolatban, és ezt most megosztom Veletek, hátha azonnal hasznát tudjátok venni. Nyugodtan szóljatok hozzá, jelezzetek vissza, hogy hogy tetszett, segített-e a ti gyerkőcötöknek.
Mitől nehezek a "nehéz tárgyak"?
Egy pedagógus édesanyával, Szilvivel beszélgettem a minap. Egyik csemetéje alsós, és az osztályban sokan nem tudnak folyékonyan olvasni, írni. Ez feszültségekhez, iskolai fegyelmezésekhez vezetett, és sok-sok nehéz pillanatot okozott a szülőknek, mivel végül mi vagyunk azok, akik az egész napi loholás után még átvesszük a tanító szerepet is, ha kell. Tisztelet és elismerés ezért minden szülőnek!!!!
Szilvi arra jött rá, hogy egy bizonyos módszerrel oktatták a gyerekeknek az olvasást, majd siettették őket, hogy hangosan és gyorsabban olvassanak órán. A módszer lényege az volt, hogy kis kártyákat mutattak fel nekik, amin tárgyak, állatok, növények voltak, mindegyiken egy darab, majd alatta kiírva az adott dolog. Próbálták elérni, hogy a kártya láttán a gyerek arra a betűsorra asszociáljon.
Persze volt erre számos magyarázat, hogy a módszer miért fantasztikus, de tény hogy emiatt és a későbbi siettetés miatt sokan olvasni sem tanultak meg rendesen, hiszen keverték egymással a dupla betűket, vagy a p, b, d betűket, melyek – ha őszintén belegondolunk- , ránézésre nagyon hasonló szimbólumok.

A módszer, ami sikeresnek bizonyult
Szilvi úgy rakta ezt helyre jó néhány gyereknél, hogy
- egyedileg rájött, melyik betűk keveréséről van szó,
- azokat gyurmából elkészíttette a gyerekekkel és
- kérte őket, hogy olyan betűs dolgokat is gyurmázzanak vagy rajzoljanak le.
Hatalmas és átütő volt a siker a gyerekeknél.
Emellett abbahagyták az alsósok stresszelését, siettetését olvasás közben, így a gyerekeknek módjuk nyílt rendesen ránézni a szavakra és kiolvasni azokat.
Lehet, hogy ennyire egyszerű a diszlexia megoldása?
Szerintem egy próbát mindenképp megér.

Mi a helyzet az egyéb tantárgyakkal? Matek, fizika, kémia, történelem...
Furcsa mód a probléma egészen hasonló tőről ered a többi tantárgynál is, mint kiderült. Az a sok szimbólum. Nem érti, mi az a gyök jel. Megpróbálod elmondani neki, hogy arra van, hogy „gyököt vonunk”, de ezt sem érti. Talán úgy lenne érdemes, hogy
– Nem érted mi a „gyök kilenc”?
Ez azt mondja röviden, hogy „Melyik számot szorozzuk meg önmagával, hogy kilenc legyen a vége?” Ezt a kérdést rövidítik úgy, hogy „gyök kilenc”, érted már?
Ugyanez a probléma a legtöbb nehéz tárgynál: a sok nem teljesen értett szimbólum és kifejezés, egymás hegyén hátán.
Gyakran észre sem veszik a gyerek, mit nem értenek pontosan, vagy olyan gyorsan történik az új fogalmak és szimbólumok bevezetése, hogy nem tudják végiggondolni, mert a korábbi még nincs fogalmi szinten begyakorolva. Ettől kifejezetten butának érezhetik magukat és amikor segíteni próbálsz, gyakran azt mondják, hogy értik már, mert szégyellik, hogy még mindig nem értik igazán.
Példák Neked, hogy lásd hogy működik a dolog
Számodra egyszerű lesz:
Egy fiatal azért volt nagyon gyenge fizikából, mert nem értette, miért van mindennek annyi jele. T=s/v. Bemagolta, hogy „s” az út, de az km, m, cm és mm is! Félreértései forrását kiszúrtuk nála és rendbe raktuk az egészet. A gyerek nagyon-nagyon butának gondolta magát, de miután kitisztítottuk nála a fogalmakat lépésről-lépésre, egyenesen megtáltosodott! És nemcsak fizikából! Önbizalma és teljesítménye az összes többi reál tárgyban is nőtt.

Még a szülőnek is nehéz lehet, viszont erre biztos emlékszel:
„Á alapú logaritmus bé jelenti az a nemnegatív valós számot, amire át emelve bét kapom.” Az első reakciónk, talán kivétel nélkül: „Mi vaaaan?” Jogos!
A nemnegatív valós szám, az a cé. Á a céediken egyenlő bével. Bármelyik kettőt tudod, jó vagy! A harmadikat kitalálod. Még mindig kavarcos? Valós szám…. Nnna, ezek azok a számok, amik használhatók, amikor pontokat akarunk kijelölni egy koordinátarendszerben.
Tudjátok, miért vérzik el ezen a logaritmuson a legtöbb gyerek és felnőtt? A „valós szám”… próbálod megérteni és körbe hivatkoznak a meghatározások, egymásra… Na, az ilyenek látszanak bonyolultnak, amíg lesz egy tiszta elképzelésünk és be nem gyakoroljuk a fogalmat, hogy már ne kelljen gondolkoznunk, erőlködnünk, amikor meglátjuk egy mondatban.
Amikor a „valós szám” kényelmes lesz, könnyebb felfogni az egész, fenti, nyakatekert mondatot is, és végre nagy koppanással leesik, hogy miben segítenek azok a fránya táblázatok!
Remélem, nem nagyon kínoztalak meg, de kénytelen voltam valahogy demonstrálni.

Mitől könnyűek a könnyű tárgyak? - technika, rajz, ének
A gyerekek többsége ezeket a tárgyakat eléggé élvezi. Miért? Mert ahhoz, hogy valamit előállítson vagy okozzon, nem kell túl sok elméleti tudás. Bemész ének órára, dúdolnak egy dallamot és az egész osztály utánozza. Még akkor is vicces foglalatosság, ha az osztály kissé hamis. Érdekes, mert a zenéhez is létezik sok-sok elmélet, technika, szakértelem. DE azt el lehet sajátítani fokozatosan, és azonnal látszik, hogy fejlődsz. A gyerek úgy is énekelhet, és sikerélmény lehet, ha csak alap szinten érti az egészet.
A sikerre kell rágyúrnunk nála. Csináljon a tudásával valamit, és ha lehet, minden tanulási egység végén viduljon fel! (Ez igaz az otthoni tanulásra is.)
Istenem, milyen egyszerű – és emlékezetes is lenne – tortát bevinni matek órára, és úgy megértetni a törteket! Minden gyerek pillanatok alatt átlátná a lényeget, garantálom nektek! És örökre nevezetes lenne számukra az a tanóra! Valószínűleg szívükbe zárnák a tanárt….
Online anyagaimat is ezeknek az alapelveknek a figyelembe vételével állítottam össze
Szem előtt tartva, hogy levegyem a problémát a válladról, amennyire csak lehet, és mindenki boldog legyen a gyerek haladásával.
Mert…
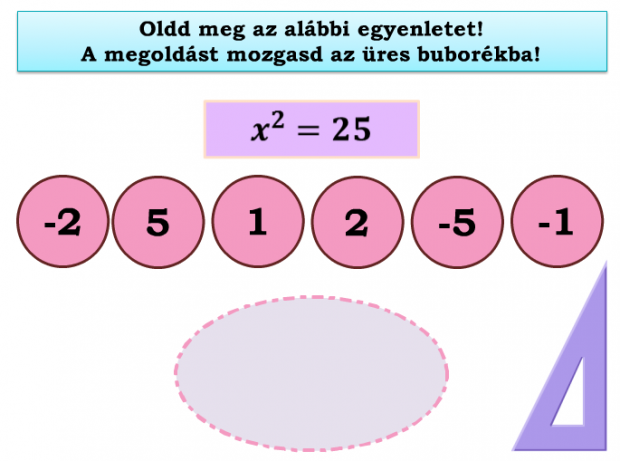
Játékos tanulással könnyebb a megértés!
Ezen az oldalon kipróbálhatjátok a gyerkőccel, hogy hogyan is működik a játékos tanulás:
Nyugodtan javasolj hozzászólásban vagy személyes üzenetben további témákat, öröm nekem ha abban segítek, amire szükséged van, és akkor, amikor szükséged van rá!
Légy nagyon-nagyon sikeres és köszönöm az érdeklődést, bizalmat!

Nagy Erika
Tanulási tanácsadó
A játékos tanulás szakértője
A Tantaki oktatóprogramok megalkotója

Kedves Erika!
A szöveg matekos részébe hiba csúszott:
Log a B = c – a alapú logaritmus b egyenlő c, az „a” a c-ediken egyenlő b! C az a szám, amire „a”-t emelve B-t kapok.
Tehát a logaritmus végeredménye a hatványkitevő.
Üdvözlettel: Juhász Jenő