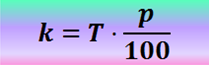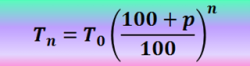Kamatos kamat

Kamatos kamatszámítás alatt azt értjük, hogy a tőkénk után kapott kamatok is tőkésítésre kerülnek, vagyis nem csak a tőkénk, hanem a tőke kamatokkal növelt értéke után kapjuk az újabb és újabb kamatokat.
Ahhoz, hogy megértsük a kamatos kamatszámítást, az egyszeri kamat kiszámítását is meg kell értenünk.
Az egyszeri kamat kiszámításának alapképlete:
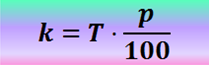
A T a kezdeti tőke, a p a kamatláb, amit el kell osztanunk százzal. Az osztás után tizedesvesszős formában írjuk fel.
Példa egyszeri kamatra:
Számítsuk ki 200 ezer Forintnak az éves kamatát, ha a kamatláb 24%!
Az előző képlet tehát úgy alakul:
k=200000*0,24=48000 Ft, vagyis 200 ezer Forint éves kamata 48 ezer Forint!
Fontos:
Ha a kamatlábot nem osztjuk el százzal, akkor máris rossz eredményt kapunk!
k=200000*24=4800000 Ft, tehát az így kapott eredmény nem jó!
Most pedig nézzük meg, a kamatos kamat kiszámításának módját:
A kamatos kamatszámítás képlete kissé eltér az egyszeri kamat képletétől:
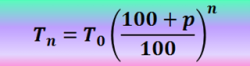
A T0 jelöli az induló tőkét, p ugyanúgy a kamatláb az n pedig az évek száma. Az eredmény a végösszeg, vagyis a már kamattal növelt alaptőke.
Fontos megjegyezni, hogy a kamatszámítási periódus végén a kamatot hozzáadják az alaptőkéhez, így a következő periódusban már a kamattal növelt alaptőke után számoljuk a kamatot.
Példa kamatos kamatra:
Kovács család 500 ezer Forintnyi megtakarítással rendelkezik. A bank 7,7%-os kamatot biztosít a lekötött összegre. Hány évre kössék le a pénzüket, ha 900 ezer Forintnyi pénzre van szükségük?
Az adatokat először kigyűjtjük:
T0=500000 Ft
Tn=900000 Ft
p=7,7% -> 0,077
n=?
Az előző képlet tehát úgy alakul:
900000=500000*(1+0,07)n => 900000=500000*1,077n
Mindkét oldalt elosztjuk 500000-rel:
1,8=1,077n
Az n-túgy kapjuk meg, hogy mindkét oldal 1,077 alapú logaritmusát vesszük:
Számológép segítségével egyszerű a logaritmus használata!
log1,0771,8=n => n=7,924 év~8 év.
Tehát a 8. év végén vehet fel a Kovács család 900 ezer Forintot!
Többet szeretnéd gyakorolni a kamatos kamatszámítást?
A matematika érettségin minden évben előfordul kamatszámításos példafeladat! Gyermeked hiányos matektudással rendelkezik? Próbáljátok ki az Érettségire Fel! oktatóprogramot ami 700 gyakorlófeladattal járul hozzá a sikeres felkészüléshez! Könnyen érthető magyarázattal és rövid elmélettel gyermeked az összes matematikai szabályt megértheti.
Kattints a képre, tudj meg még többet erről az érettségi felkészítő letölthető oktatóprogramról!

Kipróbálnád a felkészítő program demó változatát? Kattints a demó elindítása gombra, és teljesen ingyenesen kipróbálhatod a számítógépes gyakorlóprogramot:

Próbáld ki Te is a tanulás játékos oldalát!