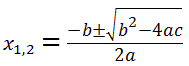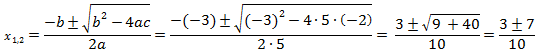Másodfokú egyenlet
Ahogy gyermeked növekszik, évről évre egyre nehezebb tananyaggal találkozik. Ugyanez igaz a matematikában is. 5. osztályban megismeri a törteket, utána egyenletekkel foglalkozik, 7. osztályban már a geometriát boncolgatják, 9. osztályban pedig új témakörként tanulják a nevezetes azonosságokat.
Az egyik legösszetettebb témakör az egyenletek témaköre. Mit is jelent az egyenlet szó? Az egyenlet a matematikában egyenlőségjellel összekapcsolt két kifejezést jelent. Érettségiig elkísérnek, és számtalan fajtájuk létezik: elsőfokú, másodfokú, harmadfokú és így tovább. Az algebra egyik legfontosabb fogalma.
Gyermeked 10. osztályban ismerkedik meg a másodfokú egyenlettel. Az egyenlet különlegessége, hogy egyik oldalán négyzetes tag is előfordul, míg a másik oldalán nulla van. Az egyenlet eredményét gyököknek nevezzük, és a gyökök száma lehet kettő, egy vagy nulla is.
A másodfokú függvény általános képlete: ax2 + bx + c=0, ahol a≠0.
Az a,b,c betűket együtthatóknak nevezzük: az a x2 együtthatója. Ezek alapján a b x együtthatója, a c pedig konstans állandó, vagyis rögzített szám, értéke nem változik.
A másodfokú egyenletnek létezik egy úgynevezett megoldóképlete. A képletben négyzetgyököt alkalmazunk, és az eredménye azt adja meg, hogy a függvény melyik két pontban metszi az x tengelyt. Előfordulnak olyan esetek is, amikor a függvény csak egy pontban metszi a tengelyt, és létezik olyan példafeladat is, amiben nem érinti az x tengelyt a függvény.
A megoldóképlet egyenlete:
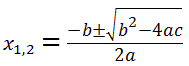
A négyzetgyök alatti részt diszkriminánsnak nevezzük, és D betűvel jelöljük. A Diszkrimináns jelentése döntő tényező, és ez adja meg, hogy a másodfokú egyenletnek hány gyöke van.
A diszkrimináns képlete: D = b2 - 4ac
Ha D>0, akkor az egyenletnek kettő valós gyöke van. Ha a diszkrimináns egyenlő nullával, akkor pontosan egy valós gyöke van, és ha kisebb nullánál, akkor az egyenletnek nincs valós gyöke, vagyis nem érinti az x tengelyt.
Hogyan oldjuk meg a másodfokú egyenletet?
1. lépés:
Az alábbi másodfokú egyenletet szeretnénk megoldani: 5x2 -3x -2 = 0
Az alapképletünk segítségével az adatokat rögtön írjuk fel: a = 5, b = -3 és c pedig c = -2.
2. lépés:
Következő lépésként a Diszkrimináns képletét kell használnunk. Helyettesítsük be a három paramétert az egyenletbe:
D2 = (-3)2 -4 ∙ 5 ∙ (-2) = 9 + 40 = 49.
Ahhoz, hogy a diszkrimináns értékét megkapjuk, gyököt kell vonnunk. √49=7. Tehát 7 nagyobb, mint nulla, így az egyenletnek 2 valós gyöke lesz.
Nem szabad elfelejteni, hogy ha egy negatív előjelű számot emelünk négyzetre, akkor zárójelbe kell tennünk. A diszkrimináns második tagjánál a negatív előjel, a 2 negatív szorzandó tag összeszorzása miatt pozitív előjelűre változik.
3. lépés:
Továbbiakban a diszkrimináns értékeként kapott számot és a paramétereket kell behelyettesítenünk a másodfokú egyenlet megoldóképletébe.
a=5, b=-3, c=-2, D=7.
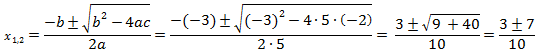
Ilyenkor bontjuk fel az egyenletet két gyökre:
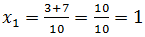,tehát az egyik gyök eredménye 1.
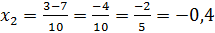,tehát a másik gyök eredménye -0,4.
Az egyenlet gyökei tehát: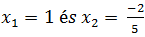 
4. lépés:
Az egyenlet gyökeit behelyettesítjük az alapképletünkbe, így le tudjuk ellenőrizni, hogy jól számoltunk-e.
Az első gyök behelyettesítése: 5 ∙ (1)2 - 3 ∙ (1) -2 = 5 -3 -2 = 0.
A második gyök behelyettesítése: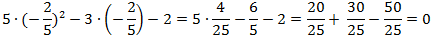 
Tehát mindkét gyök behelyettesítése után nulla lett az eredmény, vagyis jól számoltunk. Gyermeked mostantól könnyen el tudja dönteni, hogy egy másodfokú egyenletnek hány valós gyöke van.
Gyermeked 10. osztályos és bizonyos témaköröket kevésbé ért? A Tantaki Matekból Ötös oktatóanyag 10. osztályosoknak készült változatával minden témakört megtanulhat. Fontos, hogy a tizedikes tananyagot maximálisan megértse, mert a hátralévő két évben újabb és újabb ráépülő témakörökkel fog megismerkedni!
Gyermeked nem szeret tanulni? Próbáljátok ki a Matekból Ötös oktatóanyagot és gyermeked szívesen ül majd le tanulni!
Tanuljon gyermeked is a Matekból Ötös 10. osztályosoknak
készült oktatóanyagból! 600 példafeladat,
melyekkel az egész éves tananyagot gyakorolhatja újra és újra!
