Amikor egyenletekkel dolgozunk, és egyre bonyolultabb matematikai műveletek szerepelnek bennük, akkor nagyon praktikus, ha le tudjuk egyszerűsíteni azokat a lehető legkönnyebben értelmezhető formára.
Ahhoz, hogy ezt az egyszerűsítést ne legyen annyira hosszadalmas megtenni, a matematikában felfedezték az úgynevezett azonosságokat. Ezek a nevezetes azonosságok segítenek tehát neked abban, hogy ne kelljen mindig minden négyzetre emelést, szorzatot stb. részletekbe menően elvégezni ahhoz, hogy közelebb juss az eredményhez. Helyette, ha megjegyzed a legfontosabb azonosságokat, és az egyenletekben felfedezed ezeket, sok-sok időt takarítasz meg magadnak.
Azokat az egyenleteket nevezzük azonosságoknak, amelyekben minden betű helyére beírva egy számot, igaz egyenlőséget kapunk.
Például: 2(x + 3) = 2x + 6 egy azonosság, mert x helyére bármely számot írva igaz egyenlőséget kapunk.
DE: 2(x + 3) = x + 7 nem azonosság, mert csak x = 1 esetén kapunk igaz egyenlőséget.
Most pedig nézzük meg, melyek a nevezetes azonosságok!
(a + b)2 = (a + b)(a + b)
= a·a + a·b + b·a + b·b
= a2 + ab + ab + b2
= a2 + 2ab + b2
Tehát:
(a + b)2 = a2 + 2ab + b2
Nagyon fontos megjegyezni, hogy (a + b)2 NEM EGYENLŐ a2 + b2-tel!
(a − b)2 = (a − b)(a − b)
= a·a + a·(−b) − b·a − b·(−b)
= a2 − ab − ab + b2
= a2 − 2ab + b2
Tehát:
(a − b)2 = a2 − 2ab + b2
(a + b)(a − b)
= a·a + a·(−b) + b·a + b·(−b)
= a2 − ab + ab − b2
= a2 − b2
Tehát:
(a + b)(a − b) = a2 − b2
A fenti nevezetes azonosságokat nagyon jól kell tudni!
Végezd el a négyzetre emelést: (x + 3)2 = ?
Ebben a példában az első nevezetes azonosságot kell alkalmaznunk, vagyis ezt:
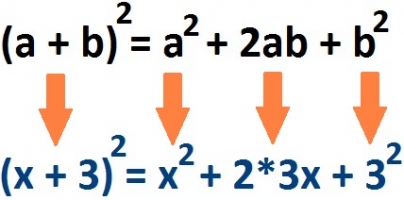Tehát az első azonosság alapján kellett felbontanunk a zárójelet.
Most pedig már csak annyi a dolgunk, hogy összevonjuk a kapott eredményt, illetve hogy négyzetre emeljük a 3-at.
(x + 3)2 = x2 + 2·3x + 32 = x2 + 6x + 9
Próbáld ki Te is a Nevezetes azonosságok gyakorlóprogramot, amely 30 oldalon keresztül valóban érthetően elmagyarázza a nevezetes azonosságok alkalmazását, és 110 interaktív, játékos feladattal addig gyakoroltatja ezt a témakört, ameddig álmodból felkeltve is helyesen tudsz számolni!
A nemzeti alaptanterv szerint az alábbi osztályokban fordul elő a nevezetes azonosság mint témakör, így a Tantaki oktatóprogramjaiban is megtalálod ezeket:
„A barátnőm juttatta el nekem a tájékoztatót a kiadványról. Azonnal felkeltette a figyelmünket, miután a 11. osztályos matematika problémája a mi lányunkat is érinti. Sajnos ezen a szinten már nem tudunk segíteni neki, ezért örültünk meg nagyon, hogy ez az oktatóanyag majd megteszi helyettünk!
Azt mi is láttuk, hogy egyszerűen, áttekinthetően magyarázza a feladatokat, de a végső döntést lányunk lelkesedése hozta meg. Örömmel ült a géphez, tudta követni és meg tudta oldani a demo feladatait!! Ezúton is köszönjük a remek csapatnak, hogy megálmodták és létrehozták az oktatóanyagot!
Első körben az alapcsomag + kombinatorikát rendeltük meg, reméljük a későbbiekben is hozzáférhetőek lesznek a programok!”
Nuber Ildikó, 2016. 12. 09.
Jelenleg itt vagyok:
Nevezetes azonosságok_tartalom