Sorozatok
A matematika elég összetett tantárgy: egyenletek, szöveges feladatok, és geometria is egyaránt előfordul benne. Bizonyos témakörök megértésére kiemelt figyelmet kell fordítani, míg például a római számok egészen rövid és könnyen érthető tananyag. Vegyük példaként a sorozatok témakörét: összetett és nehéz témakör.
Mit is jelent a sorozat szó? A sorozat egy olyan függvény, amelyet a természetes számok halmazán értelmezünk. A sorozat jele az: an. A sorozat tagjait elemeknek nevezzük. A sorozatok lehetnek végesek és végtelenek is: véges sorozatoknál megadjuk azt, hogy melyik elem a sorozat utolsó tagja.
Középiskolában a számtani és a mértani sorozattal ismerkedhet meg gyermeked.
Miről szólnak a számtani sorozatok?
A számtani sorozat olyan számsorozat, amelyben bármelyik tag és az azt megelőző tag különbsége mindig állandó. Ezt az állandó különbséget nevezzük a sorozat differenciájának és d betűvel jelöljük. Jelölése: d = an+1 - an .
A differencia adja meg, hogy a sorozat növekszik vagy csökken, illetve, hogy korlátos-e vagy sem.
A sorozat első eleme a1, a tetszőleges tagja an. A sorozat bármely tagját kifejezhetjük az a1 és a d segítségével: an = a1 + (n - 1) ∙ d.
Ha három szomszédos tagot felírunk, akkor megkaphatjuk, hogy a középső tag a 2 szomszédos tag számtani közepe!
A három szomszédos tag: an-1 , an és an+1 .
A középső tagot pedig így kapjuk meg: 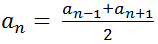
Ha tudni szeretnénk az első n tag összegét, akkor a következő képletre van szükségünk!
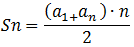
Miben különbözik a mértani sorozat?
A mértani sorozat olyan sorozat, ahol bármelyik tag és az azt megelőző tag hányadosa állandó. A hányadost kvóciensnek nevezzük és q betűvel jelöljük. A hányados csak nullánál nagyobb értékű lehet! A számtani sorozattól lényeges eltérés az, hogy míg a számtani sorozatnál hozzáadással növekszik az érték, addig a mértani sorozatnál szorzással.
A mértani sorozat tetszőleges, n-edik tagját an-nel jelöljük. Az n-edik tagot a következő képlettel kaphatjuk meg: an = a1 ∙ q(n - 1) .
A kvóciens ugyanazt a szerepet látja el, mint a differencia: megadja, hogy milyen előjelű a változás, és hogy a sorozat növekszik, vagy esetleg csökken. A három tag: 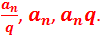
Ha három mértani tagot vizsgálunk, akkor elmondható, hogy a középső tag a két szomszédos tag mértani közepe!
A mértani sorozat első n tagjának összegét is könnyen kiszámíthatjuk az alábbi képlettel: 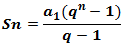
Tehát az első tag és a kvóciens segítségével könnyen kiszámíthatjuk a sorozat első n tagjának összegét.
A sorozatok témakör minden évben előfordul az érettségin is. Gyermeked a számtani sorozatokat érti, de a mértani sorozatokat már nem tudja kiszámolni? A Matekból Ötös 10. osztályos oktatóanyag segítségével megértheti a 2 sorozat közötti különbségeket és alaposan begyakorolhatja a példákat.
Gyermeked 10. osztályban ismerkedik meg bővebben
a számtani és mértani sorozatokkal!
Az oktatóanyag színes példákkal és ábrákkal illusztrálja a tananyagot!




