Valószínűségszámítás
A valószínűségszámítás a matematika egyik kiemelkedő ága. Gyermeked felső tagozatosként ismerkedik meg először a valószínűség témakörével. Gyakran előforduló példa a feldobott érme esete: Mekkora a valószínűsége annak, hogy fejet dobunk?
Próbáld ki a valószínűségszámítás gyakorlóprogramunkat most ingyenesen!
Mit is jelent a valószínűség szó? A valószínűség azt fejezi ki, hogy egy bizonyos dolog mekkora eséllyel következhet be. A hétköznapok során gyakran mondjuk azt, hogy „kevés volt az esélye”, „talán most bekövetkezik”. Ilyen esetekben a valószínűségszámítás kifejezéseit mondjuk.
Valószínűség kiszámítása
Tehát a valószínűségszámítás valamilyen esemény bekövetkezésének lehetőségével foglalkozik. Jele a P, ami a probabilitas latin szóból ered: jelentése valószínűség. Ahhoz, hogy megértsük, hogyan számoljuk ki a valószínűséget, tudnunk kell a képletét értelmezni.
Valószínűséget úgy számolunk, hogy a kedvező esetek számát elosztjuk az összes eset számával. Kedvező eseteknek azt nevezzük, ami kedvező kimenetelű esetnek számít. Például, ha társasjátékot játszunk, és csak 6-os dobásával tudunk nyerni, akkor a kedvező esetek száma 1, mivel csak a 6-os dobása jó nekünk.
Összes esetnek nevezzük a lehetséges eredmények számát, amelyeknek ugyanannyi a bekövetkezési esélye. Például dobókockával 6-féle kimenetelünk lehet, akkor az összes eset száma 6.
Valószínűségszámítás képlet: 
Példa: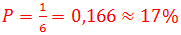 
, vagyis körül-belül 17 százalék az esélye annak, hogy hatost dobunk.
A P értéke csak 0 és 1 közötti értéket vehet fel, amit gyakran százalékos formában fejezünk ki. A valószínűségszámításnál fontos, hogy a lehetséges kimenetelek valószínűségének egyenlőnek kell lenniük. Például a dobókockás példánál mindegyik kimenetelnek 16,67% az esélye!
Nézzünk másik dobókockás példát!
Mennyi a valószínűsége annak, hogy a dobókockával páratlan számot dobok?
Az összes esetek száma 6, mivel a dobókockával 6 különböző számot dobhatunk. A kedvező esetek száma 3, mivel csak az egyes, a hármas és az ötös dobás jó nekünk. Ez három lehetséges kimenetelt jelent.
A képletünk tehát így alakul: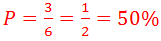 
, vagyis 50 százalék az esélye, hogy páratlan számot dobunk a dobókockával. Az alábbi példákon keresztül láthatjuk, hogy a mindennapi élet során gyakran találkozunk valószínűségszámítással. Gyermeked nem érti, hogy miért 50 % az esélye annak, hogy fejet vagy írást dob az érmével? A Valószínűségszámítás gyakorlóprogram segítségével könnyen megértheti és akár további példákat is gyakorolhat.
Rendeld meg most gyermekednek az oktatóanyagot, és gyermeked az összetettebb feladatokat is meg tudja majd oldani. Összesen 300 feladat, amit újra és újra ki lehet tölteni! Amennyiben gyermeked rosszul válaszol, a feladat helyes megoldását és annak magyarázatát is elolvashatja!
A valószínűségszámítás roppant érdekes tananyag!
Az oktatóanyag 100 oldal elmélettel és 300 gyakorlófeladattal
segít gyermekednek!
